What happens during model creation and training#
Introduction#
Halerium supports creating and training statistical models that can be described as a Bayesian network. To create such a model, one specifies the probability distribution of all the relevant random variables in the model, possibly conditional on the values of other such random variables in the model. Armed with this information, the joint probability of these model quantities taking on particular values can be constructed. Given that joint probability distribution and possibly any data on the actual values, one can then, e.g., sample from it or estimate means, variances, or the most probable values for the model quantities.
For many practical applications, that joint probability is a complicated function with a high-dimensional domain. In such cases, directly creating samples or estimating distribution moments from it is not feasible, in particular when data is provided for random variables whith distributions conditional on other random variables. Therefore, various techniques exist to approximate that joint probability and then to sample and/or estimate moments from that approximation. The process of tuning an approximation to better fit the joint probability is called model training in the context of machine learning.
When users create a halerium graph for a statistical model (either explicitly or by creating a causal structure), they specify the random variables of that model (represented by the halerium variables in the graph) and their conditional probability distributions in a way that halerium understands. When users instantiate a halerium posterior model (either explicitly or by using halerium objectives) with that graph as input, halerium constructs the joint posterior probability, i.e. the joint probability of all the model quantities taking into account any data provided for these model quantities. When users instruct halerium to solve/train the model, halerium seeks a suitable approximation to that joint posterior distribution. The details of that process and the nature of the resulting approximation are governed by the choice of model class (and sometimes additional parameters provided). When users request means or other moments from the trained model, halerium computes these moments from that approximation.
Here we discuss in more detail what happens during model creation and training by following our model for inheritance of body height, and also a simple linear regression model.
Imports#
We import the following packages, classes, and functions.
[1]:
#for handling data:
import numpy as np
# for plotting:
import matplotlib.pyplot as plt
# for graphs:
from halerium.core import Graph, Entity, Variable, StaticVariable, show
# for creating models with a factory:
from halerium.core.model import get_posterior_model
# for creating and using models directly:
from halerium.core.model import ForwardModel, MAPModel, MAPFisherModel
Model for inheritance of body heights#
Model description#
We briefly recapitulate the main points of our model for inheritance of body height. A person is modelled using two scalar random variables: their observable height in cm and a (not directly observable) genetic factor (also expressed in cm). We assume that absent any data on genetic factors or heights, a person’s genetic factor \(g\) follows a normal distribution \(\mathcal{N}(\mu_g, \sigma^2_g)\) with mean \(\mu_g=0\) and variance \(\sigma^2_g = 75\):
\begin{equation} p(g) = p_\mathcal{N}(g;\mu_g=0, \sigma^2_g=75) \qquad(1) \end{equation}
Here,
\begin{equation} p_\mathcal{N}(x;\mu, \sigma^2) = \frac{1}{\sqrt{2 \pi \sigma^2}}\exp\left[\frac{(x - \mu)^2}{2\sigma^2}\right] \end{equation}
is the probability density function of the normal distribution.
Furthermore, given the genetic factor, a person’s height \(h\) follows a normal distribution with mean \(\mu_h=\bar{\mu}_h + g\) and variance \(\sigma_h^2=25\):
\begin{equation} p(h|g) = p_\mathcal{N}(h;\mu_h=\bar{\mu}_h + g, \sigma^2_h=25) \qquad(2) \end{equation}
Here, \(\bar{\mu}_h\) is the a-priori mean height in absense of genetic factor information. We consider two types of person, i.e. women and men, which differ in their a-priori mean height:
\begin{equation} \bar{\mu}_h = \begin{cases} 167 & \text{for women, and }\\ 175 & \text{for men.} \end{cases} \qquad(3) \end{equation}
We model inheritance of body height by assuming that the genetic factor of a child \(g_c\) given the genetic factor of the mother \(g_m\) and father \(g_f\) is normally distributed with mean given by the average of the parents’ genetic factors:
\begin{equation} p(g_c| g_m, g_f) = p_\mathcal{N}\bigl(g_c ; \mu_{g_c}=\frac{g_m + g_f}{2}, \sigma_{g_c}^2=37.5\bigr) \qquad(4) \end{equation}
The distribution of the child’s height \(h_c\) given the genetic factor \(g_c\) is then again given by: \begin{equation} p(h_c|g_c) = p_\mathcal{N}(h_c;\mu_{h_c}=\bar{\mu}_h+ g_c, \sigma^2_h=25) \qquad(5) \end{equation}
Creating the halerium graph for the model#
For convenience, we create entity templates Woman and Man from prototypical woman and man instances:
[2]:
with Entity("woman") as woman:
Variable("genetic_factor", shape=(), mean=0, variance=75)
Variable("height", shape=(), mean=167 + genetic_factor, variance=25)
Woman = woman.get_template("Woman")
with Entity("man") as man:
Variable("genetic_factor", shape=(), mean=0, variance=75)
Variable("height", shape=(), mean=175 + genetic_factor, variance=25)
Man = man.get_template("Man")
Instatiating such a template, a new entity is created with random variables “genetic_factor” and “height”, which follow normal distributions (the default, if no distribution is set explicitly) with the respective means and variances. Instantiating such a template within the context (i.e. “with” clause) of a halerium graph, these random variables become part of that graph. For example, when we create a halerium graph “family” with entities “alice”, “bob”, “harry”, and “sally”, each of these four contribute their genetic factor and height to the graph “family”:
[3]:
with Graph("family") as family:
alice = Woman("alice")
bob = Man("bob")
harry = Man("harry")
sally = Woman("sally")
display(*(f"{v.global_name}" for v in family.get_all_variables()))
'family/alice/genetic_factor'
'family/alice/height'
'family/bob/genetic_factor'
'family/bob/height'
'family/harry/genetic_factor'
'family/harry/height'
'family/sally/genetic_factor'
'family/sally/height'
So far, we have not specified any particular relation between the four family members and their genetic factors. Thus currently the joint probability of the members’ genetic factors \(g_{\text{alice}}\), \(g_{\text{bob}}\), \(g_{\text{harry}}\), \(g_{\text{sally}}\) and heights \(h_{\text{alice}}\), \(h_{\text{bob}}\), \(h_{\text{harry}}\), \(h_{\text{sally}}\) reads:
\begin{align} p( g_{\text{alice}}, h_{\text{alice}}, g_{\text{bob}}, h_{\text{bob}}, g_{\text{harry}}, h_{\text{harry}}, g_{\text{sally}}, h_{\text{sally}} )&= p(g_{\text{alice}}) p(h_{\text{alice}}|g_{\text{alice}}) \times\\&\quad p(g_{\text{bob}}) p(h_{\text{bob}}|g_{\text{bob}}) \times\\&\quad p(g_{\text{harry}}) p(h_{\text{harry}}|g_{\text{harry}}) \times\\&\quad p(g_{\text{sally}}) p(h_{\text{sally}}|g_{\text{sally}}) , \qquad(6) \end{align}
where the distributions on the r.h.s. are given by Eqs. (1) and (2) thanks to the defaults in the Man and Woman templates used to create the family members.
If we assume that harry and sally are the biological children of alice and bob and want our graph to reflect this, we have to replace the means and variances for the genetic factors of harry and sally according to Eq. (4):
[4]:
with family:
harry.genetic_factor.mean = (alice.genetic_factor + bob.genetic_factor) / 2
harry.genetic_factor.variance = 37.5
sally.genetic_factor.mean = (alice.genetic_factor + bob.genetic_factor) / 2
sally.genetic_factor.variance = 37.5
As a result, the new joint probability reads:
\begin{align} p( g_{\text{alice}}, h_{\text{alice}}, g_{\text{bob}}, h_{\text{bob}}, g_{\text{harry}}, h_{\text{harry}}, g_{\text{sally}}, h_{\text{sally}} )&= p(g_{\text{alice}}) p(h_{\text{alice}}|g_{\text{alice}}) \times\\&\quad p(g_{\text{bob}}) p(h_{\text{bob}}|g_{\text{bob}}) \times\\&\quad p(g_{\text{harry}}|g_{\text{alice}}, g_{\text{bob}}) p(h_{\text{harry}}|g_{\text{harry}}) \times\\&\quad p(g_{\text{sally}}|g_{\text{alice}}, g_{\text{bob}}) p(h_{\text{sally}}|g_{\text{sally}}) , \qquad(7) \end{align}
where \(p(g_{\text{harry}}|g_{\text{alice}}, g_{\text{bob}})\) and \(p(g_{\text{sally}}|g_{\text{alice}}, g_{\text{bob}})\) are given by Eq. (4).
Creating and training the halerium model#
Halerium models implement a specific solution strategy in order to do actual numerical calculations on the statistical model described by a halerium graph.
Creating a forward model#
The simplest halerium model class is the ForwardModel:
[5]:
forward_model = ForwardModel(graph=family)
The forward model does not require any training since it does not construct any approximation to the posterior. One can task the model right away to generate examples or to compute means and standard deviations:
[6]:
g_sally_example = forward_model.get_example(family.sally.genetic_factor)
g_sally_mean = forward_model.get_means(family.sally.genetic_factor, n_samples=1000)
g_sally_variance = forward_model.get_variances(family.sally.genetic_factor, n_samples=1000)
print("sally genetic factor example:", g_sally_example)
print("sally genetic factor mean:", g_sally_mean)
print("sally genetic factor valiance", g_sally_variance)
sally genetic factor example: [0.51099806]
sally genetic factor mean: [0.57809521]
sally genetic factor valiance [80.1997469]
Mean values and variances for random variables are computed by generating samples and estimating means and variances from these samples.
The forward model generates values for all random variables in one of the two following ways and returns it. If the model was provided with data values for a random variable (none in this example so far), that value is returned. For random variables without data, the value is drawn from its distribution (using a speudo-random number generator). If a distribution parameter of a random variable depends on a another random variable, the value for that second random variable is drawn first and then used to compute the distribution parameter for the first random variable.
For example, to generate an example for sally’s genetic factor \(g_{\text{sally}}\), values for alice’s and bob’s genetic factor are drawn, then the mean for \(g_{\text{sally}}\) is computed from these values, and finally a value for \(g_{\text{sally}}\) is drawn from a normal distribution with that mean.
This implies that data provided for, e.g. alice’s genetic factor is taken into account when generating sally’s genetic factor. To illustrate that, we assume \(g_{\text{alice}} = 20\) and provide that information to our model upon creation:
[7]:
forward_model = ForwardModel(graph=family,
data={family.alice.genetic_factor: [20.]})
This now shifts the mean of sally’s genetic factor to about 10:
[8]:
g_sally_example = forward_model.get_example(family.sally.genetic_factor)
g_sally_mean = forward_model.get_means(family.sally.genetic_factor, n_samples=1000)
g_sally_variance = forward_model.get_variances(family.sally.genetic_factor, n_samples=1000)
print("sally genetic factor example:", g_sally_example)
print("sally genetic factor mean:", g_sally_mean)
print("sally genetic factor valiance", g_sally_variance)
sally genetic factor example: [0.49954011]
sally genetic factor mean: [10.24242303]
sally genetic factor valiance [55.33048614]
In the forward model, information on actual values is only carried forward and not backward (hence the name). For example, providing data for sally’s genetic factor does not seem to affect the genetic factor’s of any other family members:
[9]:
forward_model = ForwardModel(graph=family,
data={family.sally.genetic_factor: [20.]})
g_alice_example = forward_model.get_example(family.alice.genetic_factor)
g_alice_mean = forward_model.get_means(family.alice.genetic_factor, n_samples=1000)
g_alice_variance = forward_model.get_variances(family.alice.genetic_factor, n_samples=1000)
print("alice genetic factor example:", g_alice_example)
print("alice genetic factor mean:", g_alice_mean)
print("alice genetic factor valiance", g_alice_variance)
alice genetic factor example: [-4.87444787]
alice genetic factor mean: [0.11666016]
alice genetic factor valiance [73.68440255]
Creating a maximum-aposteriori (MAP) model#
Halerium provides several model classes that feature information propagation in all directions. The simplest of these is the MAPModel, which implements a gradient-based maximum posterior (MAP) finder strategy.
When a MAP model is instantiated with a halerium graph and data as input, it internally creates the joint posterior distribution as a function of the values of any random variables of the model not fixed by data.
[10]:
map_model = MAPModel(graph=family,
data={family.sally.genetic_factor: [20.]})
With that function alone, the model cannot create samples or compute means yet. The model needs to be trained first. For training, the MAP model treats the values of all random variables not fixed by data (here all variables except sally’s genetic factor) as internal parameters and maximizes the joint posterior ditribution varying these:
[11]:
map_model.solve()
The posterior maximization is done by minimizing the negative logarithmic posterior using standard gradient-based multi-dimensional local minimization algorithms. The result is a set of values for the non-fixed random variables that maximizes the posterior locally (thus for multi-modal posteriors, the answer may depend on the randomly generated initial values for the minimization).
When the model generates examples, e.g. for computing means and variances, it always returns these MAP values. Thus there is no variance in the generated examples, and the estimated variance is zero:
[12]:
g_alice_example = map_model.get_example(family.alice.genetic_factor)
g_alice_mean = map_model.get_means(family.alice.genetic_factor, n_samples=3)
g_alice_variance = map_model.get_variances(family.alice.genetic_factor, n_samples=3)
print("alice genetic factor example:", g_alice_example)
print("alice genetic factor mean:", g_alice_mean)
print("alice genetic factor valiance", g_alice_variance)
alice genetic factor example: [9.99999377]
alice genetic factor mean: [9.99999377]
alice genetic factor valiance [0.]
Creating a maximum-aposteriori (MAP)-Fisher model:#
The halerium MAPFisherModel class not only employs a gradient-based maximum posterior finder, but in addition Fisher information matrix estimates, and combines these to approximate the joint posterior by a multivariate normal distribution.
Thus, the MAP-Fisher model also returns finite variances:
[13]:
map_fisher_model = MAPFisherModel(graph=family,
data={family.sally.genetic_factor: [20.]})
map_fisher_model.solve()
g_alice_example = map_fisher_model.get_example(family.alice.genetic_factor)
g_alice_mean = map_fisher_model.get_means(family.alice.genetic_factor, n_samples=1000)
g_alice_variance = map_fisher_model.get_variances(family.alice.genetic_factor, n_samples=1000)
print("alice genetic factor example:", g_alice_example)
print("alice genetic factor mean:", g_alice_mean)
print("alice genetic factor valiance", g_alice_variance)
alice genetic factor example: [2.26739388]
alice genetic factor mean: [9.99990615]
alice genetic factor valiance [53.18391532]
Linear regression model#
Model description#
To illustrate how training halerium models is related to the model training in ‘conventional’ machine learning, we discuss a simple linear regression model.
We assume that we have a process with some quantities \(x_i\), called features, and quanities \(y_i\), called targets, for a set of examples \(i=1,2,...\) are connected via:
\begin{equation} y_i = a \,x_i + b + n_i, \qquad (8) \end{equation}
where the \(n_i\) are i.i.d. normally distributed noise with vanishing mean and variance \(\sigma_n^2\). Now the slope \(a\) and intercept \(b\) are to be estimated from our collection of examples (e.g. to predict observations of target values given feature).
Example data#
We generate some example data for the model:
[14]:
n_examples = 100
np.random.seed(42)
sigma_x = 3
sigma_a = 1
sigma_b = 1
sigma_n = 0.5
a_true = np.random.normal(0, sigma_a)
b_true = np.random.normal(0, sigma_b)
x_data = np.random.normal(0, sigma_x, size=(n_examples,))
y_data = a_true * x_data + b_true + np.random.normal(0, sigma_n, size=(n_examples,))
print("true a =", a_true)
print("true b =", b_true)
plt.plot(x_data, y_data, '.');
plt.xlabel('x');
plt.ylabel('y');
true a = 0.4967141530112327
true b = -0.13826430117118466
Conventional machine learning approach#
Standard linear regression sets up the loss function
\begin{equation} L(a,b; x, y) = \frac{1}{2} \sum_i (y_i - a \,x_i - b)^2 \qquad (9) \end{equation}
and employs, e.g. a gradient method to find the values for \(a\) and \(b\) that minimize the loss \(L\).
For linear regression with regularization, the loss is extended by regularization terms involving \(a\) (and sometimes \(b\)), e.g. \(l^2\) regularization:
\begin{equation} L(a,b; x, y) = \frac{1}{2} \sum_i (y_i - a \,x_i - b)^2 + \frac{a^2}{2\sigma_a^2} + \frac{b^2}{2\sigma_b^2} \qquad (10) \end{equation}
where \(\sigma_a^2\) and \(\sigma_b^2\) are regularization-strength hyper-parameters.
Bayesian network approach#
From a Bayesian network perspective, Eq. (8) implies, that the probability \(p(y_i | x_i, a, b)\) of obtaining target value \(y_i\) given feature value \(x_i\), slope \(a\) and intercept \(b\) is given by a normal pdf:
\begin{equation} p(y_i | x_i, a, b) = p_{\mathcal{N}}(y_i; \mu_{y_i}= a \,x_i + b, \sigma^2_{y_i} = \sigma^2_n). \qquad (11) \end{equation}
To turn this into a full Bayesian network model, we also assume some prior distribution for \(a\) and \(b\), e.g.
\begin{align} p(a) &= p_{\mathcal{N}}(a; 0, \sigma^2_{a}), \text{ and} \qquad (12)\\ p(b) &= p_{\mathcal{N}}(b; 0, \sigma^2_{b}). \qquad\quad\;\; (13) \end{align}
We also have to specify \(p(x_i)\), but its details won’t be of concern if we assume that the value for \(x_i\) is always given by data. We are then equipped to write down the joint distribution,
\begin{equation} p(a, b, x, y) = p(a) p(b) \prod_i p(x_i) p(y_i|x_i, a, b), \qquad (14) \end{equation}
and its’ negative logarithm,
\begin{equation} -\ln p(x, y, a, b) = \frac{1}{2} \sum_i (y_i - a \,x_i - b)^2 + \frac{a^2}{2\sigma_a^2} + \frac{b^2}{2\sigma_b^2} - \sum_i \ln p(x_i). \qquad (15) \end{equation}
Thus training a halerium MAPModel or MAPFisherModel with this graph and data results in the same estimates for the slope \(a\) and intercept \(b\) as a standard linear regression model with \(l^2\) regularization.
There are several advantages of the Baysian halerium model over conventional regression models:
There is no need for special treatment of missing values (such as removing incomplete examples or performing imputation).
The trained halerium model can not only be used to predict features given targets, but also targets given features. Thus there is no need to also train a reverse model.
If a
MAPFisherModelis employed (or, e.g., anADVIModel,MGVIModel, orMCMCModel), one also directly obtains uncertainties on \(a\) and \(b\) (without having to perform train-test-split validation or cross-validation).
Creating the halerium graph for the model#
The halerium graph for the simple linear regression model can be directly witten as (there are also convenience functions described in the notebook on regression):
[15]:
with Graph("lr_graph") as lr_graph:
x = Variable("x", shape=(), mean=0, variance=sigma_x**2)
a = StaticVariable("a",shape=(), mean=0, variance=sigma_a**2)
b = StaticVariable("b",shape=(), mean=0, variance=sigma_b**2)
x = Variable("y", shape=(), mean=a*x + b, variance=sigma_n**2)
Note that the regression parameters \(a\) and \(b\) as well as the features and targets are defined as scalars, i.e. with shape=(). The actual number of examples (and thus the dimensions of the feature and target data vectors) will be fixed when instantiating the halerium model. Also note that the features and targets are defined as Variable, so they can have a different value for each example, whereas the regression parameters are defined as StaticVariable, so they are assumed
taking on the same value for all examples.
Creating and training a halerium model#
MAP model#
The MAP model is quickly set up and trained with the data generated above:
[16]:
map_model = MAPModel(graph=lr_graph,
data={lr_graph.x: x_data,
lr_graph.y: y_data})
map_model.solve()
When the model is instantiated, the negative log. probability according to the halerium graph is constructed, resulting in an expression equivalent to Eq. (15). When the model is trained, the values for \(a\) and \(b\) are adjusted to minimize that negative log. probability.
The values found by the model are:
[17]:
a_estimated = map_model.get_means(lr_graph.a)
b_estimated = map_model.get_means(lr_graph.b)
print("estimated a =", a_estimated)
print("estimated b =", b_estimated)
print("true a =", a_true)
print("true b =", b_true)
estimated a = 0.4736983304278624
estimated b = -0.1217203455949462
true a = 0.4967141530112327
true b = -0.13826430117118466
MAP-Fisher model#
The MAP-Fisher model also yields posterior uncertainties on the model parameters:
[18]:
map_fisher_model = MAPFisherModel(graph=lr_graph,
data={lr_graph.x: x_data,
lr_graph.y: y_data})
map_fisher_model.solve()
a_estimated = map_fisher_model.get_means(lr_graph.a)
b_estimated = map_fisher_model.get_means(lr_graph.b)
a_uncertainty = map_fisher_model.get_standard_deviations(lr_graph.a)
b_uncertainty = map_fisher_model.get_standard_deviations(lr_graph.b)
print("estimated a =", a_estimated, "+/-", a_uncertainty)
print("estimated b =", b_estimated, "+/-", b_uncertainty)
print("true a =", a_true)
print("true b =", b_true)
estimated a = 0.47369833976688425 +/- 0.018788827587077814
estimated b = -0.12172032575668985 +/- 0.050823746789473746
true a = 0.4967141530112327
true b = -0.13826430117118466
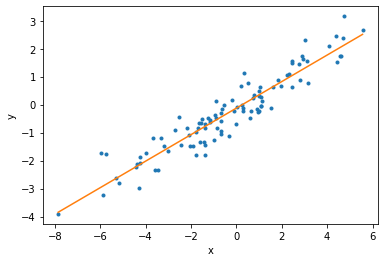
[19]:
min_x = np.min(x_data)
max_x = np.max(x_data)
plt.plot(x_data, y_data, '.');
plt.plot([min_x, max_x], [a_estimated * min_x + b_estimated, a_estimated * max_x + b_estimated]);
plt.xlabel('x');
plt.ylabel('y');
[ ]: