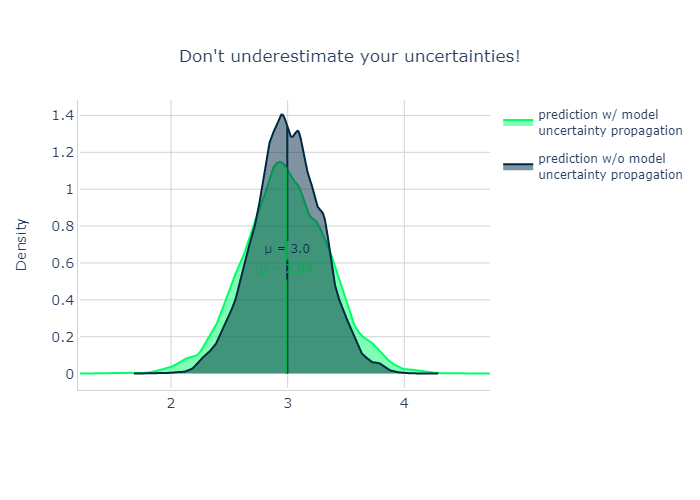
Model uncertainty propagation

The total uncertainty is composed out of two contributions: - the intrinsic uncertainty of the modelled process - the uncertainty about the values of the model parameters

Let’s demonstrate this with an artificial model

Create a simple graph that just relates two variables x and y

import numpy as np
import halerium.core as hal
from IPython.display import Image

g = hal.Graph("g")
with g:
    x = hal.Variable("x", mean=0, variance=.1)

    factor = hal.StaticVariable("factor", mean=0., variance=1.)
    log_var = hal.StaticVariable("log_var", mean=-2., variance=1.)
    var = hal.exp(log_var)
#    var = hal.StaticVariable("var")
#    var.mean = hal.exp(log_var)
#    var.variance = 0

    y = hal.Variable("y")
    y.mean = x * factor
    y.variance = var

# call this to show the graph in the online platform
# hal.show(g)

Create artificial training data

real_factor = 3. # the actual value of the parameter
real_log_var = np.log(0.3**2)

dl_gen = hal.DataLinker(n_data=10)
dl_gen.link(g.factor, real_factor)
dl_gen.link(g.log_var, real_log_var)
model_gen = hal.get_generative_model(g, dl_gen)

x_train, y_train = model_gen.get_samples([g.x, g.y], n_samples=1)
x_train, y_train = np.array(x_train)[0,:], np.array(y_train)[0,:]

Now train a model with the training data

dl_train = hal.DataLinker(n_data=len(x_train))
dl_train.link(g.x, x_train)
dl_train.link(g.y, y_train)

model_train = hal.get_posterior_model(g, dl_train)
rec_factor = model_train.get_means(g.factor)
std_factor = model_train.get_standard_deviations(g.factor)
rec_log_var = model_train.get_means(g.log_var)
std_log_var = model_train.get_standard_deviations(g.log_var)

print("real_factor:", np.round(real_factor, 2))
print("rec_factor: {} +-{}".format(np.round(rec_factor, 2), np.round(std_factor, 2)))
print("real_log_var:", np.round(real_log_var, 2))
print("rec_log_var: {} +-{}".format(np.round(rec_log_var, 2), np.round(std_log_var, 2)))

real_factor: 3.0
rec_factor: 2.99 +-0.2
real_log_var: -2.41
rec_log_var: -2.43 +-0.42

import pylab as pl
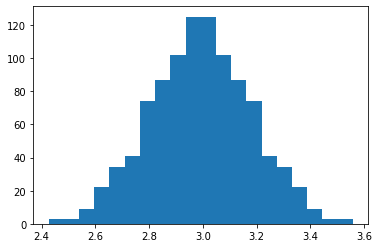
pl.hist(model_train.get_samples(g.factor, n_samples=1000), bins=20)

display(model_train.get_means(g.factor, n_samples=1000))
display(model_train.get_standard_deviations(g.factor, n_samples=1000))

2.992204822110734

0.18626433575347545

Predict without uncertainty propagation

# predict without uncertainty propagation by linking the reconstructed parameter values

x_test = [1.]

dl_predict1 = hal.DataLinker()
dl_predict1.link(g.factor, rec_factor)
dl_predict1.link(g.log_var, rec_log_var)
dl_predict1.link(g.x, x_test)

model_predict1 = hal.get_generative_model(g, dl_predict1)
prediction_samples_without_uncertainty = model_predict1.get_samples(g.y, n_samples=5000)
prediction_samples_without_uncertainty = np.array(prediction_samples_without_uncertainty)[:,0]

Predict without uncertainty propagation

# predict with uncertainty propagation by using the get_posterior_graph method

posterior_graph = model_train.get_posterior_graph()

dl_predict2 = hal.DataLinker()
dl_predict2.link(g.x, x_test)

model_predict2 = hal.get_generative_model(posterior_graph, dl_predict2)
prediction_samples_with_uncertainty = model_predict2.get_samples(g.y, n_samples=5000)
prediction_samples_with_uncertainty = np.array(prediction_samples_with_uncertainty)[:,0]

from plots import plot_two_densities

Image(plot_two_densities(prediction_samples_with_uncertainty, prediction_samples_without_uncertainty,
                   smoothness=8.))